跟题解的推法不太一样。这确实是道非常有 AtCoder 风格的题。

首先看到这种一眼没有多项式做法的题，考虑找性质简化问题。

我们注意到有 条 的边是永远不会被删去的，考虑以此为突破口，观察与其方向相同的负边的性质。

Key observation：如果我们确定了一条从 到 的负边必须保留，那么对于 ，，负边 在最优解中也必须保留。

证明：考虑证明加入这条边后不影响合法性，如果保留边 之后出现了负环，那么把这个环中所有走过 的部分都替换为先用 边从 走到 ，再走边 ，然后从 用 边走到 ，就会得到一个不经过边 的负环，说明加入这条边之前也有负环，矛盾了。

既然不影响合法性，所有边权值还都 ，那加入这条边显然会得到一个更优的解。

所以，最终答案的负边一定连成如下形式：

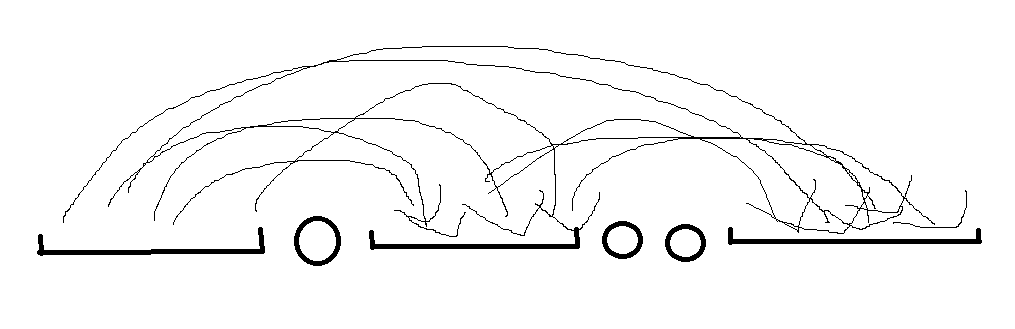
其中线段表示序列上的一个个区间，区间内部不连边，圆点表示一些孤立点。所有非孤立点向在它后面与其不同区间的非孤立点都有连边。

进一步观察可以发现，孤立点是不存在的，因为将孤立点并入其旁边的区间肯定不劣，这个操作不会影响正边怎么连。

于是在最优解中，原序列可以被划分为 个区间 ，满足 。所有起点终点在同一个区间内的负边都要删掉。而此时能保留的正边 必须满足 与 在同一个区间或者 所在区间与 所在区间中间没有夹着其它区间。其余的正边都要删掉。

问题转化到这里就很好做了。设 表示考虑到第 位，最后一个区间是 的最小代价。 可以从 转移过来，转移时加的代价可以通过二维前缀和快速预处理。总时间复杂度为 。

#include <bits/stdc++.h>
using namespace std;
const int N = 5e2 + 5;
typedef long long ll;
template<typename T> inline bool ckmin(T &x,const T &y) { return (x > y) && (x = y,true);}
int n;
int B[N][N],A[N][N]; // A+,B-
ll dp[N][N];
ll sa[N][N],sb[N][N];
inline ll Query(ll s[N][N],int l1,int r1,int l2,int r2) {
	if(l1 == 0 && l2 == 0) return s[r1][r2];
	if(l1 == 0) return s[r1][r2] - s[r1][l2 - 1];
	if(l2 == 0) return s[r1][r2] - s[l1 - 1][r2];
	return s[r1][r2] - s[l1 - 1][r2] - s[r1][l2 - 1] + s[l1 - 1][l2 - 1];
} 
int main() {
	cin >> n;
	for(int i = 1;i <= n;i++) {
		for(int j = 1;j < i;j++) cin >> A[j][i];
		for(int j = i + 1;j <= n;j++) cin >> B[i][j];
	}
	for(int i = 1;i <= n;i++)
		for(int j = 1;j <= n;j++)
			sa[i][j] = sa[i][j - 1] + sa[i - 1][j] - sa[i - 1][j - 1] + A[i][j],
			sb[i][j] = sb[i][j - 1] + sb[i - 1][j] - sb[i - 1][j - 1] + B[i][j];
	memset(dp,0x3f,sizeof dp);
	ll ans = 1e18;
	dp[0][0] = 0;
	for(int i = 1;i <= n;i++)
		for(int j = 1;j <= i;j++)
			for(int k = 0;k < j;k++)
				ckmin(dp[j][i],dp[k][j - 1] + Query(sb,j,i,j,i) - Query(sa,j,i,j,i) - Query(sa,k,j - 1,j,i));
	for(int i = 1;i <= n;i++) ckmin(ans,dp[i][n]);
	ans += sa[n][n];
	cout << ans << endl;
	return 0;
}