非常好题目，不会第一步。

令 。

考虑 固定的时候怎么做。

把所有数按照 从大到小排成一排。此时贪心选最大的 肯定是错的，因为如果第二大的 马上就要被 Bot 吃掉，而最大的 并不急着被吃，我们先选第二大的肯定比先选最大的优。

不妨换个角度考虑，对于 A 选的一个位置集合 ，其合法当且仅当 ，因为在其前面，我们至少要选 个位置。

那么贪心策略就容易得出了。维护一个优先队列，按 从小到大，每次把两个数加入优先队列，然后 A 选出优先队列中最大的那个数并弹出就是答案。

观察上述过程，发现其只取决于 的相对大小关系，所以可以设 表示第 大的数在多少种方案中被选择，最后答案就是 。

但”第 大的数“还是难以考虑，不妨考虑“前 大的数”，故设 表示前 大的数被选择次数之和。然后，我们把”前 大的数“视为 ，其余视为 。问题变成计数所有的 序列中，一共 pop 了多少个 。注意，我们在这里认为 和 ， 和 之间没有区别，最后将方案乘上 即可。

考虑计算 ，设第 轮插入时给优先队列提供了 个 ，显然 ，且 。设 表示当前优先队列中一共有几个 。在经过第 轮插入后，。我们设 ，并将 看成二维平面上的点。那么一轮插入就等价于向右走一步，并向上走 步，且在 时有 的系数 （因为 时原排列有两种填数的方案）。如果走到了 轴以下，就强行扳回 轴。如下图：

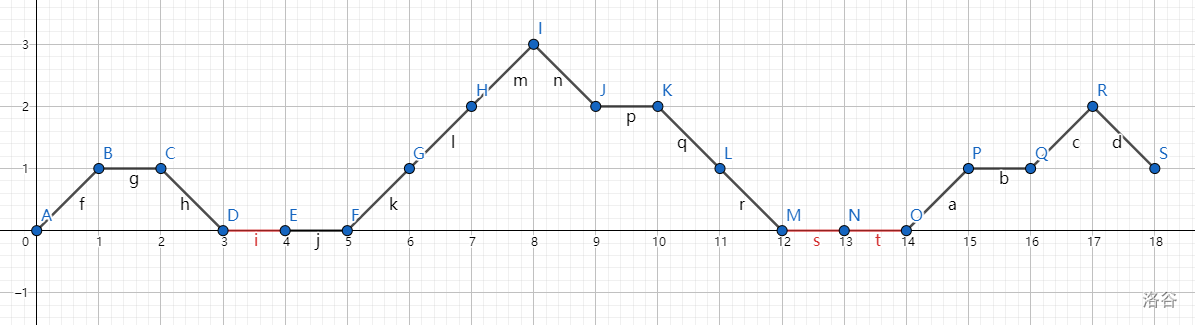
其中红边表示扳回 轴的步数。一次扳回等价于我们在优先队列中 pop 了一个 。所以用 减去红边个数就得到了 pop 的个数。

这种不断对 chkmax 有一个转化：我们不妨允许路径走到 轴一下，此时路径会停在 ，同时原先 chkmax 的位置就等于现在纵坐标的前缀最小值位置，如下图：

因为 ，所以前缀最小值每次变少时都只会减少 。也就是说，一条路径中的红边个数，就是最低点纵坐标的相反数。

设 ，显然最低点纵坐标在 之间取。枚举 ，我们要计算路径最低点纵坐标 的方案数。差分，变为路径不越过直线 的方案数。

引理 ：从 走到 ，且每一步向右上/向右/向右下的方案分别为 ，那么总方案数为 。

证明：方案数等于

那么，路径不越过直线 的方案数，可以运用经典的折线法计算。我们把限制变为”不经过 “，那么对于每一条经过 的路径，我们把该条路径与 的第一个交点前面的部分，沿 翻折，它就映射到了一条从 开始， 结束的一条任意路径。容易证明这个映射是双射。那么不合法路径方案数就是

所以，路径纵坐标最小值 的方案数就是 。

所以最小值 的方案数就是 。

那么我们就可以列出 的计算式了： 这个 中的组合数上指标是固定的，预处理之后容易做到 计算。

那么最后答案就是 了！

时间复杂度 。不可多得的好题。

const int N = 1e6 + 5,P = 998244353;
inline void Plus(int &x,const int &y) { x += y;if(x >= P) x -= P;}
int n,a[N];
int fac[N],ifac[N];
int bs[N];
inline void init(int n)
{
	fac[0] = 1;
	for(int i = 1;i <= n;i++) fac[i] = 1ll * fac[i - 1] * i % P;
	ifac[1] = 1;
	for(int i = 2;i <= n;i++) ifac[i] = 1ll * ifac[P % i] * (P - P / i) % P;
	ifac[0] = 1;
	for(int i = 1;i <= n;i++) ifac[i] = 1ll * ifac[i - 1] * ifac[i] % P;
}
inline int C(int n,int m) { if(n < 0 || m < 0 || n < m) return 0;return 1ll * fac[n] * ifac[m] % P * ifac[n - m] % P;}
int g[N];
int main()
{
	read(n);
	for(int i = 1;i <= n;i++) read(a[i]);
	sort(a + 1,a + n + 1,greater<int>());
	n /= 2;
	init(n + n);
	for(int i = 2 * n;i >= 0;i--)
		bs[i] = bs[i + 2],Plus(bs[i],C(n + n,i));
	for(int m = 0;m <= n + n;m++)
	{
		int p = max(0,n - m);
		g[m] = 1ll * (n - p) * C(n + n,m + p + p) % P;
		Plus(g[m],P - (m + p + p + 2 <= n + n ? bs[m + p + p + 2] : 0));
		g[m] = 1ll * g[m] * fac[m] % P * fac[n + n - m] % P;
	}
	int ans = 0;
	for(int i = 1;i <= n + n;i++)
		Plus(ans,1ll * a[i] * (g[i] - g[i - 1] + P) % P);
	cout << ans << endl;
	return 0;
}