感觉比 22 年出得阳间一些,D4T1 (通信题) 和 D4T2 (最小内向森林)
不会做,没有这两题的题解。
有些好题会尽量写得详细。
D1T1 两种货币
注意到原图是棵树,那么从 到
的路径只有一条,用主席树+二分处理路径信息即可。
Submission
D1T2 JOI 国的节日 2
一道较难的好题。
首先明确:
- 最优策略是按
排序之后贪心选。
- 最后算答案时,用总数减去 fake 解等于最优解的方案数。
这种将区间作为计数对象的 DP ,一般会尝试设 表示 DP 到第 个位置,前 个位置一共有
个还未闭合的左端点作为状态。下文把这些左端点叫做“接口”。
在这题,我们可以变通一下:设 ,表示 DP 到 第 个位置,设在
之前,最靠右的被选入最优解的区间的右端点 为 ,在 以前有
个接口(下文称其为“无用接口”,因为它们不会影响最优解),在 以后有 个接口(下文称其为“有用接口”)。 分别表示:
:当前 fake
解没有比最优解少一个区间,但在 fake
策略下无可用接口(即不存在一个接口使得 连向该接口后 fake 解变大)。
: 当前 fake
解没有比最优解少一个区间,且在 fake 策略下有可用接口。
:当前 fake
解比最优解少一个区间,且在 fake 策略下有可用接口。
我们没有记录 fake
比最优少且无可用接口的情况,因为这种情况不可能转移回 fake
等于最优的情况。
需要指出的是,fake 只可能有
个可用接口,因为如果有的话,必须是 fake
解最靠右的那个区间右边最靠左最左的接口,要不然与 fake
的求解方式相矛盾。
转移分类讨论,即可做到 。
考虑优化。发现
这一维的存在根本不会影响最优解与 fake
解的情况,只是在转移的时候贡献了一个系数。
所以考虑状态中只记录 ,如果某次转移产生了新的
个无用接口,就直接在后面钦定
个右端点拼上去,转移到 ,系数是 。
时间复杂度 ,空间需要滚动数组。因为 ,实现时要卡一下 的上下界。
附一张图帮助理解状态: 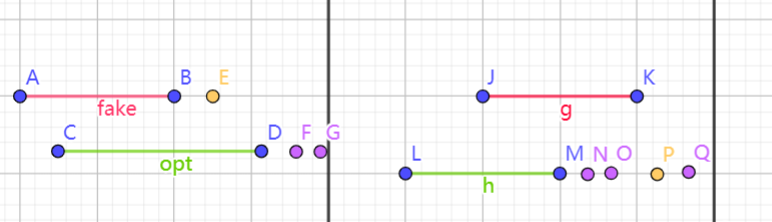
图中,红线代表 fake
解中最靠右的区间,绿线代表最优解中最靠右的区间,紫色代表 这一维所记录的接口,黄色代表 fake
策略的可用接口,黑色的竖线代表当前 DP 到的位置 。
图左侧是 fake 比最优解少
的情况,右侧是 fake 解与最优解相等的情况。右侧的黄色接口也被算入 这一维中。
理解状态之后,相信转移分讨起来不是很困难。
Submission
D1T3 护照
考虑如果只要到达
的所有国家怎么做,因为每次可达的点都是一段区间,我们只需能到达 号点即可。问题变为由 向 中所有点连边,求 到 的最短路。线段树优化建图即可。
回到原问题,我们可以求出 到
和 到 的最短路,然后令 。这么做有一个问题就是我们会重复计算一些区间,也就是这两条最短路径可能在一开始出现重复部分。
对于边 ,显然有 ,那么我们如果发现
的,就用 来更新 。如此往复,这样就可以保证 的正确性。
如何实现这个操作呢?我们把所有
都丢进一个堆里,每次取出最小的进行松弛即可。这类似一个多源最短路的过程。
Submission
D2T1 传送带
考虑链怎么做。每隔三个点放一个点(这样任意两个产品就不会走到一起了),然后看最后这个点的产品走到哪。每次把已经知道的边的方向调整一下,使其不影响我们对未知边的询问即可。
树的思路也差不多。考虑把点按照
分类,取出点数最多的那一类,每个点放一个产品。这样一次询问之后,放了一个产品的点最少可以确定一条邻边。如果一个点的所有邻边都被确定,我们就将其删去。选择类的时候选出未被删去的点数最多的那一类即可。
每次询问都能至少确定 的边,询问次数上界为 。
Submission
D2T2 议会
对于一个人
,如果选他当议长,那么选副议长
的时候,只有那些原来票数就等于 ,且 投了票的议案会从通过变成不通过。那么设
没投票的议案集合为 。选 做议长时,票数等于 的议案集合为
。去掉一些可以快速计算的部分之后,我们只需对每个
算出 即可。
显然上式等价于 。忽略 的限制,只需先做一遍超集和,再做一遍子集和即可。现在要 ,我们只需在统计子集信息时,记录答案最大值、次大值、以及编号与最大值不同的集合中最大的大小即可。
Submission
D2T3 水羊羹 2
首先有一个暴力 DP
的思路,但是这个状态一点也不优美,看上去很难以拓展到原问题。
先发现一个性质:小段长度一定为 。否则可以调整使得不劣。
下文把将一个数作为一个小段称作“选这个数”。
假如我们现在钦定选 ,那下一个选的位置显然要在满足条件的情况下尽量靠前,设其为
。
设 表示最大的 满足 ,,即
和 可以同时选。
那么 就是最小的满足 的 (注意我们这里没写 ,因为如果 ,我们可以把 调整到 的位置,显然也是不劣的,所以 就能取得更小)。
那么我们选小段的过程,就是从
开始向后跳跃, 的过程。
如果不带修的话,可以用个倍增维护跳跃的步数。
如果带修的话,我们需要一个观察:如果 存在,。
实际上你考虑
递增的情况就能很容易发现这个性质。
那么单点修改 就只会改变至多
个 ,且单步跳跃长度也不超过 。
于是可以写一棵线段树维护跳跃。每个区间记录前
个点在区间内最远跳到的位置和步数即可。
时间复杂度 。
Submission
D3T1 合唱
首先,我们只关注一个序列能够形成的最少的曲目数,因为一个大曲目可以被拆成若干个小曲目。
经过手玩可以发现,不管曲目如何安排,从左往右第 个 A 一定配上第 个 B。
进一步地说,如果我们要让第 个 A 唱一首歌,那么第 个 B 就要移到这些 A 的后面,设 表示第 个 A 前面有多少个 B,那么对于 ,其就对代价有 的 贡献。
同时可以发现不同曲目之间的代价没有影响,因为一个曲目的移动不会影响后面曲目的
。
那么设 表示前 个 A 唱了 首歌的最小代价,就有 。
设 表示 的最大 ,并将 对 取 。设后面这个 为 。设 的前缀和为 。那么有 。
证明
函数满足四边形不等式是简单的,拆开之后发现除了 的项都可以消掉。根据 Itst
的博客,可以说明答案关于歌曲数目存在凸性。
那就可以 wqs 二分解决曲目个数的限制,内层 DP 形如 ( 是二分的斜率)。斜率优化 DP
即可。
时间复杂度 。
好题啊。
D3T2 曲奇
