CF1229F 题解

First Post:

Last Update:

CF1229F 题解

除了官方题解，我在百度上还没有搜到关于这题比较详细的描述，故写篇题解造福社会，希望对读者有益。

题意：给出 个数 ，在一个环上均匀分布着 个点，每个点初始有 张牌。你一次操作可以选择一个点，将其上的一张牌移到与其相邻的位置，花费 的代价。求最少的代价，使得调整完后，第 个点上的牌数在 之间。

。

首先考虑断环为链。

具体地，设 表示由 向 运送的牌数（ 可以为负，这等价于由 向 运送 张牌），特别地， 为由 向 运送的牌数。

那么断环为链，就是钦定 为一个特定的值 ，即把这条边的决策先做掉。

那么向后做的时候，设 表示钦定 ，且第二张，第三张，...，第 张牌均已经满足条件的最小代价。

考虑 如何从 转移过来。

首先，会有限制：。

即 。（特别地，）

令

对应到 上就是 。

用滑动窗口转移就可以把这个 DP 做到 。

进一步优化的话，需要发现这个 的性质，这也是为什么，我把 DP 数组写成函数的形式，而非二维数组。

考虑到，我们每次对 的操作是：将每个点替换成包含它的一段区间的最小值，给 加上一个凸函数。

容易归纳证明，对于任意 ， 都是凸函数。

既然看出来了是凸的，我们不妨考察斜率，我们发现一次 的操作，会把一段的斜率减小 ，另一段的斜率增大 。总的来看，斜率总是会在 之间。

那么可能的斜率数量也很有限。

那么我们不妨从这一点入手来维护这个凸函数：维护这个函数的所有拐点。

拐点是什么呢？就是你考虑到这个函数是凸的，且呈现明显的分段特征，每段内部是一条直线，且直线的斜率从左往右单调递增，我们维护的就是每一段的端点。

我们接下来称这类凸函数为“折线”。

类似下图：

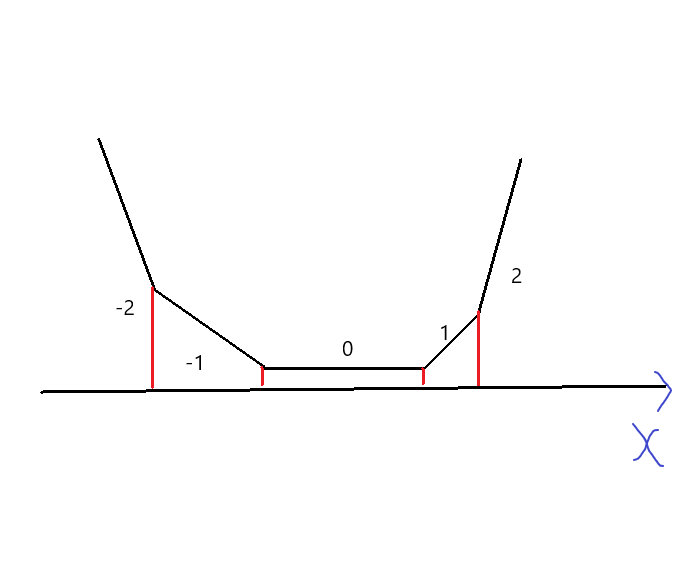
这是一个折线，其中红线代表拐点，即两段之间的分界点，数字代表每一段的斜率。

我们发现，只要维护了拐点集合，那么两个拐点之间的斜率也可以推得，具体地，我们同时维护斜率 和斜率 的拐点集合 ，那么每相邻三个拐点所对应的两段函数，斜率就会相差 ，如果实际上这两段的斜率差 ，那么我们就重复加入一些拐点，使其满足上面的条件即可。（比如说， 中最大拐点与次大拐点之间的直线斜率就是 ，再往左是 ，以此类推）

现在我们维护了拐点集合，考虑我们的操作对其产生的影响。

再次整理我们的操作：

  1. 令 为 ，将 替换为 。
  2. 令 为 ，将 替换为 。
  3. 取出 的区间最小值（因为 有个范围）

设 中间那段斜率为 的段为 。

考虑操作 。

对于 ，

对于 ，。

否则，。

画个图就可以知道，我们相当于把函数左半边向左平移 ，把函数右半边向右平移 。对于中间那段斜率为 的，我们相当于将其伸长了。

反应在拐点上，就是 中的数同时减去 ， 中的数同时加上 。用两个数维护平移量即可。

考虑操作 。

我们把 拆成两个函数：。

这两个函数分别对应 的左右半边，我们以 为例，来讲述怎么处理。

这相当于我们将一个折线加上一条斜率为 的射线。

分类讨论：

  1. 如果 ，那么画图可得， 中的直线没有任何变化，而对于 中的点，如果其在 的左边，那么它那里的直线斜率要 。因为一个拐点就表示了一次斜率的变化，我们直接将 这个点加入 即可。
  2. 否则，我们会发现， 中的一些直线的斜率会减 ，比如说， 这一段的斜率就从 变成了 。我们发现，除开这一段以外，其它的在 左边的直线斜率都减小了 ，但正负号没变。那我们把 从 中弹出，加入 中，并将 加入 中即可。

加上 是一样的。

考虑操作 ：

首先我们要知道 的全局最小值，即斜率为 的那一段的函数值，这个可以在操作 中顺带维护出来。

那么考虑询问区间 和斜率为 的区间 的关系。

如果它们有交，直接输出 即可。

否则，假设 在 左边，容易发现 （因为这一段的斜率都小于 ）。

考虑从 到 中间的那些折线，因为我们已经维护了拐点集合，可以方便地将其提取出来，斜率也是可以算的。

那直接从 一路推到 即可。

和 都可以用两个堆维护，本人偷懒写了个 set。

具体可以看代码。

好了，现在我们会了 确定的情况了，那环怎么做呢？

结论：设 表示一个 所对应的最小代价，那么 关于 也是凸的。

证明大概分为两部分：

  1. 证明如果 的取值范围是实数，那么不改变最优解。
  2. 证明：如果 和 都是 的一组最优解，那么 也是一组最优解。这可以推出

所以，我们对 进行一个三分即可。

本题总时间复杂度为 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
#include <bits/stdc++.h>
using namespace std;
const int N = 3.5e4 + 5;
typedef long long ll;
int n,a[N],L[N],R[N];
struct Heap{
	multiset<ll> S;
	ll tag;
	inline void clear() { S.clear();tag = 0;}
	inline void insert(ll x) { S.insert(x - tag);}
	inline void erase(ll x) { S.erase(S.find(x - tag));}
	inline void shift(ll x) { tag += x;}
	inline ll Greatest() { return tag + *S.rbegin();}
	inline ll Lowest() { return tag + *S.begin();}
	inline int size() { return S.size();}
};
Heap ql,qr;
long long ans = 0;
inline void addL(ll x) // x - t
{
	if(x <= qr.Lowest()) {ql.insert(x);return;}
	ll tmp = qr.Lowest();
	qr.erase(tmp);ql.insert(tmp);qr.insert(x);
	ans += x - ql.Greatest();
}
inline void addR(ll x)
{
	if(x >= ql.Greatest()) { qr.insert(x);return;}
	ll tmp = ql.Greatest();
	ql.erase(tmp);qr.insert(tmp);ql.insert(x);
	ans += qr.Lowest() - x;
}
inline ll GetVal(ll l,ll r) // 折线的区间最值
{
	if(l <= qr.Lowest() && ql.Greatest() <= r) return ans;
	if(l > qr.Lowest())
	{
		long long delta = 0;
		long long lst = qr.Lowest();qr.erase(lst);qr.insert(l);
		int K = 1;
		while(qr.size() && qr.Lowest() <= l)
			delta += 1ll * K * (qr.Lowest() - lst),
			lst = qr.Lowest(),qr.erase(lst),++K;
		return ans + delta;
	}
	if(r < ql.Greatest())
	{
		long long delta = 0;
		long long lst = ql.Greatest();ql.erase(lst);ql.insert(r);
		int K = 1;
		while(ql.size() && ql.Greatest() >= r)
			delta += 1ll * K * (lst - ql.Greatest()),
			lst = ql.Greatest(),ql.erase(lst),++K;
		return ans + delta;
	}
}
inline ll Solve(ll x1)
{
	// printf("x1:%lld\n",x1);
	ql.clear();qr.clear();ans = abs(x1);
	for(int i = 1;i <= n + 1;i++)
		ql.insert(x1),qr.insert(x1);
	for(int i = 2;i <= n;i++)
	{
		int dl = L[i] - a[i],dr = R[i] - a[i]; //[x - dl,x + dr]
		ql.shift(-dr);qr.shift(-dl);
		addL(0);addR(0);
	}
	// puts("done\n");
	//  L_1 \le a_1 - x_1 + x_n \le R_1
	ll nowl = L[1] - a[1] + x1,nowr = R[1] - a[1] + x1;
	// printf("%lld %lld %lld\n",nowl,nowr,ans);
	// printf("ql: ");
	// for(auto it : ql.S) printf("%lld ",it + ql.tag);printf("\n");
	// printf("qr: ");
	// for(auto it : qr.S) printf("%lld ",it + qr.tag);printf("\n");
	ll res = GetVal(nowl,nowr);
	// printf("res:%lld\n",res);
	return res; 
}
int main()
{
	cin >> n;
	for(int i = 1;i <= n;i++)
		cin >> a[i] >> L[i] >> R[i];
	ll lef = -1e18,righ = 1e18;
	while(righ - lef > 5)
	{	
		ll lmid = (lef + righ) >> 1,rmid = lmid + 1;
		if(Solve(lmid) < Solve(rmid)) righ = rmid;
		else lef = lmid;
	}	
	ll ans = 1e18;
	for(ll i = lef;i <= righ;i++)
		ans = min(ans,Solve(i));
	cout << ans << endl;
	return 0;
}

本题中，维护折线的技巧有一个好听的名字：Slope trick，我们通过拐点集合，恰当地表示出了折线的信息，且让操作变得十分简单，虽然这个转化本身比较抽象。（

类似的题目还有：CF713C，ABC217H，ARC123D

≡