CF1770G 题解（分治 NTT 在格路计数中的应用）

First Post:

Last Update:

之前没有接触过这方面的应用（没想到分治 NTT 这么强大），故记录一下。

首先我们考虑一个格路计数模型，即从 出发，向右或向上走，要走到 ，但第 列只存在行数不大于 的点， 单调不降，且 ，求路径条数。

上述的网格是个阶梯状的图形，用分治 NTT 解决阶梯网格的格路计数是很经典的应用（虽然此前我从来没听说过）。

首先考虑 DP，这是简单的，即 。

但是直接这么做很难优化，本质上是因为这个 DP 没有明显的阶段性，即同一个 内的所有 都会互相转移。

我们修改 DP 状态，第一维记录 ，第二维记录 ，那么就会有 。

为了避免在 的时候还会有 的限制，考虑从 开始沿左上-右下方向把阶梯网格劈成两半，计算从 和 走到这条斜对角上的点 （） 的方案数，容易发现这两个问题是对称的。

综合上述分析，我们将问题转化为，从 出发，每次可以向右或向右上走一步，且在第 列只存在行数不大于 的点，走到最后一列每一个点的方案数。容易证明转化完后的 仍然是不降的，且满足一个优秀的性质：。

事实上，转化后的 就是 的点的个数，就算这个阶梯形网格是个 的矩形， 也不超过 。

经过上述的转化之后，问题终于有了明显的分层，可以考虑优化转移了。

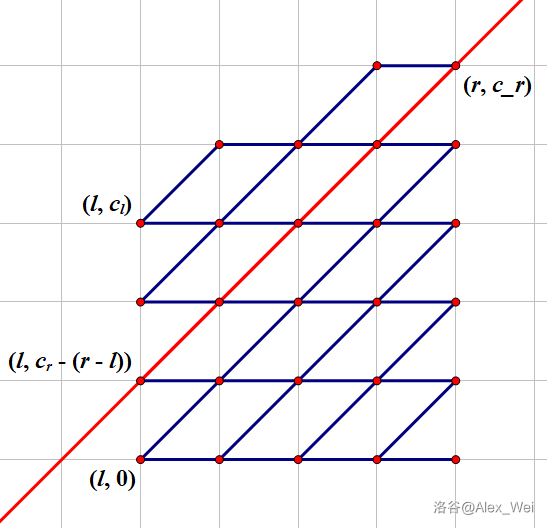
考虑一个 对 的贡献，设 ，我们发现，对于 ， 转移到 时不会受到 的限制（因为 ）。

（图源自 @Alex_Wei，对于 的部分，它就算一路往上冲，也不会超过上图的红线。）

那么从 转移到 的系数算起来就很容易了，就是 。

这是一个很明显的卷积形式，我们设 ，那么我们将 与 进行卷积， 将这一部分贡献加到 上。

对于 的 ，我们尝试将区间分为 和 递归处理，即先将左区间的贡献加到 上，再用 的一部分去更新 。

把这两部分的贡献加起来，所有 的 对 的贡献就计算完毕了。

考虑实现这么一个算法流程：

设 表示当前还没确定 值的区间为 ，传入多项式的第 项表示 ，返回多项式的第 项表示 。这也可以看作是让所有 的 全部减去 ，传入的 ，返回的 。下文将采用这种视角进行叙述。

设 ，对于 ，将 与 卷积，将得到的结果加到 上面。

对于 ，分治下放，设 ，那么顺次执行 。

将最后得到的 也加到 上面。然后返回 即可。

对于边界， 的处理是平凡的。

分析复杂度。对于下传的 ，其长度显然不超过 ，也就是说，对于 ， 的长度不会超过当前分治区间的父区间的长度，即 。设 同阶，则该算法复杂度与一般的分治 NTT 相同，为 。

终于可以说回原题了。

题意：给出一个括号串 ，设 为最少需要删去的字符数使得原串是个合法括号串，求删去 个字符后原串合法的方案数，对 取模。

。

首先，我们要删去的字符一定形如 ))))(( ，即一段右括号再加上一段左括号。

我们考虑找到这个分界点。

把左括号看成 ,右括号看成 。考察这个序列的前缀和。

我们一定一个位置为 的，当且仅当它对应的数是前缀最小值。因为 位置的数一定是在它之前的位置的数的最小值减 ，所以每遇上一个 位置，我们就需要在这个位置或其之前删掉一个右括号。

那我们就将最后一个 位置，当作上述的分界线，在这个位置左边，我们只删右括号；在这个位置右边，我们只删左括号。

这两个部分是本质相同的，下文以删右括号的部分为例。

那么我们对于每个前缀，选中的右括号数一定不小于 位置的数量。

那么我们可以设 表示前 个右括号 ，选中的右括号数减去 位置的数量为 的方案数。

如果 是个 位置，转移到 ，否则转移到 。

这看上去就挺格路计数的，可以套用上面的做法。因为限制只有 ，我们甚至不需要记录 。

当然，还是稍有变形。具体地，记录 中 位置的个数 。那么对于 ， 转移到 就不受 限制的影响，转移系数为 。

对于 的部分，递归下放去做即可，下放的多项式长度不会超过 ，故复杂度为 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
#include <bits/stdc++.h>
using namespace std;
const int N = 1 << 20,P = 998244353,G = 3;
inline int Add(int a,int b) { return (a + b >= P) ? (a + b - P) : (a + b);}
inline int Sub(int a,int b) { return (a < b) ? (a - b + P) : (a - b);}  
inline int qpow(int a,int b) { int res = 1;while(b) {if(b&1) res = 1ll * res * a % P;a = 1ll * a * a % P;b >>= 1;} return res;}
const int Gi = qpow(G,P - 2);
int n;
char s[N];
int Gs[N],Gs2[N];
int rev[N];

inline int GetLen(int x)
{
	int len = 1;
	while(len <= x) len <<= 1;
	return len;
}
inline void calc_rev(int len)
{
	for(int i = 0;i < len;i++)
	{
		rev[i] = rev[i >> 1] >> 1;
		if(i & 1) rev[i] |= len >> 1;
	}
}
int fac[N],ifac[N];
inline void init(int len)
{
	for(int i = 1;i < len;i <<= 1)
	{
		Gs[i] = Gs2[i] = 1;
		Gs[i + 1] = qpow(G,(P - 1) / (i << 1));
		Gs2[i + 1] = qpow(Gi,(P - 1) / (i << 1));
		for(int j = 2;j < i;j++)
			Gs[i + j] = 1ll * Gs[i + j - 1] * Gs[i + 1] % P,
			Gs2[i + j] = 1ll * Gs2[i + j - 1] * Gs2[i + 1] % P;
	}
	fac[0] = 1;
	for(int i = 1;i < len;i++) fac[i] = 1ll * fac[i - 1] * i % P;
	ifac[1] = 1;
	for(int i = 2;i < len;i++) ifac[i] = 1ll * ifac[P % i] * (P - P / i) % P;
	ifac[0] = 1;
	for(int i = 1;i < len;i++) ifac[i] = 1ll * ifac[i - 1] * ifac[i] % P;
}
inline int Binom(int n,int m) { if(n < 0 || m < 0 || n < m) return 0;return 1ll * fac[n] * ifac[m] % P * ifac[n - m] % P;}
inline void NTT(vector<int> &F,int len,int type)
{
	assert(F.size() <= len);
	F.resize(len);
	for(int i = 0;i < len;i++)
		if(i < rev[i]) swap(F[i],F[rev[i]]);
	for(int k = 1;k < len;k <<= 1)
		for(int j = 0;j < len;j += k + k)
			for(int i = 0;i < k;i++)
			{
				int cur = type == 1 ? Gs[k | i] : Gs2[k | i];
				int u = F[i | j],v = 1ll * cur * F[i | j | k] % P;
				F[i | j] = Add(u,v);
				F[i | j | k] = Sub(u,v);
			}
	if(type == -1)
		for(int i = 0,Inv = qpow(len,P - 2);i < len;i++)
			F[i] = 1ll * F[i] * Inv % P;
}
vector<int> t; // 存储每个要删的括号的标记状态
void Solve(int l,int r,vector<int> &f)
{
	if(l == r)
	{
		if(!t[l])
		{
			f.push_back(0);
			for(int i = f.size() - 1;i >= 1;i--)
				f[i] = Add(f[i],f[i - 1]);
		}
		else for(int i = 0;i < f.size() - 1;i++) f[i] = Add(f[i],f[i + 1]);
		return;
	}
	int mid = l + r >> 1,len = r - l + 1,cnt = 0;
	for(int i = l;i <= r;i++)
		cnt += t[i];
	vector<int> res(f.size() + (len - cnt),0);
	if(f.size() > cnt)
	{
		vector<int> A(f.size() - cnt,0),B(len + 1,0);
		for(int i = 0;i < f.size() - cnt;i++)
			A[i] = f[i + cnt];
		for(int i = 0;i <= len;i++)
			B[i] = Binom(len,i);
		int L = GetLen(f.size() + len - cnt);
		calc_rev(L);
		NTT(A,L,1);NTT(B,L,1);
		for(int i = 0;i < L;i++) A[i] = 1ll * A[i] * B[i] % P;
		NTT(A,L,-1);
		for(int i = 0;i < res.size();i++) res[i] = A[i];
	}
	vector<int> ff0(min((int)f.size(),cnt),0);
	for(int i = 0;i < ff0.size();i++) ff0[i] = f[i];
	Solve(l,mid,ff0);Solve(mid + 1,r,ff0);
	for(int i = 0;i < ff0.size();i++) res[i] = Add(res[i],ff0[i]);
	f = res;
}
int DoIt()
{
	if(t.empty()) return 1;
	vector<int> f(1,1);
	Solve(0,t.size() - 1,f);
	return f[0];
}
int main()
{
	scanf("%s",s + 1);
	n = strlen(s + 1);
	int cur = 0,lst = 0;
	init(GetLen(n * 2 + 2));
	for(int i = 1;i <= n;i++)
		if(s[i] == '(') ++cur;
		else { if(!cur) lst = i;else --cur;}
	cur = 0;
	for(int i = 1;i <= lst;i++)
		if(s[i] == '(') ++cur;
		else { if(!cur) t.push_back(1);else t.push_back(0),--cur;}
	int ans = DoIt();
	vector<int>().swap(t);cur = 0;
	for(int i = n;i > lst;i--)
		if(s[i] == ')') ++cur;
		else { if(!cur) t.push_back(1);else t.push_back(0),--cur;}
	ans = 1ll * ans * DoIt() % P;
	cout << ans << endl;
	return 0;
}

这道题加深了我对分治 NTT 的理解。

≡