本题就当是对 Slope trick 的入门了。

首先考虑 不大的情况。

设 表示在 子树内，点燃时间为 的最小代价。

那么考虑合并 和一个儿子 ，则有 。（ 是 与 之间的边权）

我们令 。

可以证明， 是关于 的下凸函数，且每一段的斜率均为整数。

设 表示 斜率为 的那一段的左右端点的横坐标，那么 变化如下： 具体分析如下：

对于第一种情况：因为在 处 ， 的斜率小于等于 ，即修改 以下的边的代价 ，那肯定不如直接修改 （代价恰为 ），所以在这里直接把 修改到 ，然后取出在 点的函数值。

对于第二种情况：函数在 处取到最小值，我们跟第一种情况的理由一样，能够修改 就别修改 中的 ，所以 中的 一定 ，而为了让 修改的代价尽量小，我们直接把 拉到 。这样就是最优的了。

第三种情况较为简单，第四种情况与第一种类似，就不再赘述。

对于这种斜率为整数的下凸壳，我们可以通过维护拐点和最右边的直线来表示这个凸壳。

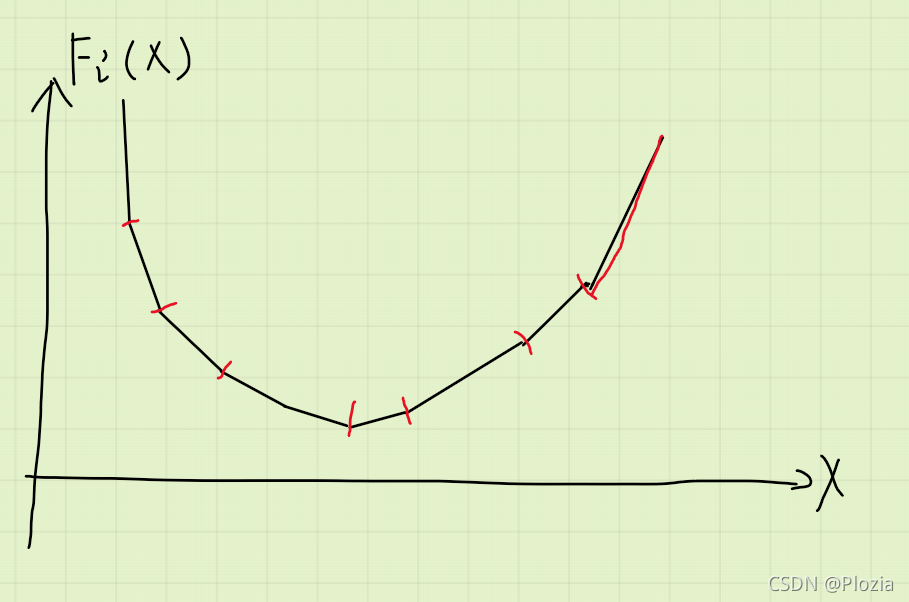
就像上图，我们只需维护所有的红点和红线即可。

我们默认每三个相邻拐点所表示的两条直线的斜率差都是 ，如果不是，那我们就多次加入同一个拐点。

如何求一个点 的函数值 呢？因为拐点的斜率差都是 ，我们用 减去在 之前的所有拐点的横坐标即可。

如何执行 呢？还是因为拐点序列的性质，我们直接把二者的拐点序列按顺序拼接起来即可。

现在我们有了这个凸壳模型，我们考虑上面的操作是如何把 变为 的。

首先，把 左边的部分向上平移 ，然后把 这一部分整体向右平移 ，并在 处插入一条斜率为 的直线，把原函数 的部分的斜率都变为 。

注意到函数的斜率最大值也只有 ，我们甚至不需要“维护那条红线”，处理所有的拐点即可。

考虑这些操作怎么办：

1. 向上平移 ，这等价于 ，而 不论是从这里来看，还是从定义上看，都显然是所有边权的和，所以这个很简单。
2. 把大于 的部分的斜率都变为 。这个可以在所有的 都并入 之后再行处理。注意到每个 有且仅有一个斜率为正的拐点 ，假设 的儿子有 个，那么合并完之后就有 个斜率为正的拐点，那么弹出 个最大的拐点即可。
3. 把 向右平移一个 ，这个只需要删除拐点 ，加入拐点 即可。
4. 插入一条斜率为 的直线，这个在第三项中其实就已经处理完了。

以上操作都可以用一个可合并的大根堆维护，写个左偏树即可。

#include <bits/stdc++.h>
using namespace std;
const int N = 6e5 + 5;
typedef long long ll;
struct node{
	int lc,rc,dis;
	ll val;
}tr[N];
int Merge(int x,int y)
{
	if(!x || !y) return x + y;
	if(tr[x].val < tr[y].val) swap(x,y);
	tr[x].rc = Merge(tr[x].rc,y);
	if(tr[tr[x].lc].dis < tr[tr[x].rc].dis) swap(tr[x].lc,tr[x].rc);
	tr[x].dis = tr[tr[x].rc].dis + 1;
	return x;
}
inline int Pop(int x) { return Merge(tr[x].lc,tr[x].rc);}
int rt[N];
int n,m;
int fa[N],C[N],sons[N];
int main()
{
	cin >> n >> m;
	for(int i = 2;i <= n + m;i++)
		cin >> fa[i] >> C[i],++sons[fa[i]];
	ll ans = 0;
	int tot = 0;
	for(int i = n + m;i > 1;i--)
	{
		ll l = 0,r = 0; // 维护斜率为 0 的那些线段
		if(i <= n) // 非叶
		{
			while(--sons[i]) rt[i] = Pop(rt[i]);
			r = tr[rt[i]].val;rt[i] = Pop(rt[i]);
			l = tr[rt[i]].val;rt[i] = Pop(rt[i]);
		}
		tr[++tot].val = l + C[i];
		tr[++tot].val = r + C[i];
		rt[i] = Merge(rt[i],Merge(tot,tot - 1));
		rt[fa[i]] = Merge(rt[fa[i]],rt[i]);
	}
	for(int i = 2;i <= n + m;i++) ans += C[i]; // f(0)
	while(sons[1]--) rt[1] = Pop(rt[1]);
	while(rt[1]) ans -= tr[rt[1]].val,rt[1] = Pop(rt[1]);
	cout << ans << endl;
	return 0;
}