这看上去是较为经典的轮廓线模型了。我思考的时候都一直想到怎么从一条折线变化到另一条折线了，还是没有想到正解简洁的 DP 状态。

首先有暴力的 做法，直接暴力判断两条线是否越过。

但 DP 时每次加入一条线，这种转移的颗粒度太大，考虑每次加入小一点的对象，加入一次走步，这样虽然状态可能多一点，但转移复杂度降下去了。基于这个思路，我们考虑怎么设计状态使得其能够适配这个转移。

设 表示当前填到了第 条折线的第 段 （ 从 到 ），记录一个二进制数 。 显然要记录前 步都时怎么走的，那 记录啥呢？我们暂时令其记录“从当前位置开始的限制”，也就是说，从当前位置开始填的线不能越过 代表的线。

如何转移呢？如果当前 为 且可以往左走，就转移 表示往左走。同理， 可以往右走时，也转移 。

余下的问题就是当 且往右走时，新的 怎么产生。此时你会发现，当前走的路径与分界线不再重合，而我们对 后半部分的定义是依赖于“当前位置”的。

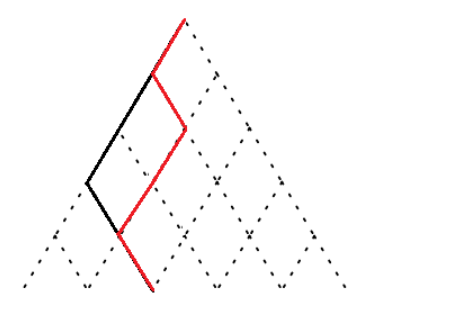
(图源 @StayAlone 题解)

如图，黑色为旧的分界线，我们在第二层的第一个位置产生了分叉，分界线也要相应调整。具体地，我们找到 后面第一个向右走的位置，把中间这一段向左倾斜的线平移过来。这样分界线又和当前位置重合了，且不会损失任何应被算入答案的解。

找到 " 后面第一个向右走的位置" 可以使用 函数。未尽细节详见代码，不再赘述。

#include <bits/stdc++.h>
using namespace std;
const int N = 25,Sz = 1 << 20,P = 1e9 + 7;
inline void Plus(int &x,const int &y) { x += y;if(x >= P) x -= P;}
inline int lowbit(int x) { return x & (-x);}
int n,m,q;
int A[N * N],B[N * N],C[N * N];
int Lims[N][N];
int dp[2][N][Sz];
int main() {
	cin >> n >> m >> q;
	for(int i = 0;i <= m;i++)
		for(int j = 0;j < n;j++) Lims[i][j] = 2;
	for(int i = 1;i <= q;i++) 
		cin >> A[i] >> B[i] >> C[i],Lims[A[i]][B[i] - 1] = C[i];
	dp[1][0][0] = 1;
	int op = 1;
	for(int i = 1;i <= m;i++,op ^= 1) {
		for(int j = 0;j < n - 1;j++) 
			for(int s = 0;s < (1 << n - 1);++s) {
			// 往左走
			if((~s >> j & 1) && Lims[i][j] != 1)
				Plus(dp[op][j + 1][s],dp[op][j][s]);
			// 往右走 
			if(Lims[i][j] != 0) {
				if(s >> j & 1) Plus(dp[op][j + 1][s],dp[op][j][s]);
				else {
					int p = lowbit(s >> j + 1) << j + 1;
					Plus(dp[op][j + 1][(s ^ (1 << j)) - p],dp[op][j][s]);
				}
			}
		}
		for(int j = 0;j <= n - 1;j++) for(int s = 0;s < (1 << n - 1);++s)
			dp[op ^ 1][j][s] = 0;
		for(int s = 0;s < (1 << n - 1);++s)
			dp[op ^ 1][0][s] = dp[op][n - 1][s];
	}	
	int ans = 0;
	for(int s = 0;s < (1 << n - 1);++s) Plus(ans,dp[op ^ 1][n - 1][s]);
	cout << ans << endl;
	return 0;
}